Hacking Google Random Number Generator
One of the most widely used random number generators must be the one built into Google. But how random is it? Can you rely on it for your daily dose of entropy?
Feeling lucky?
Google random number generator runs in the browser and works like this
apparently_random = Math.floor(Math.random() * (max - min + 1)) + min;
The source of perceived randomness comes from Math.random(). After taking a look at the docs, this note rings a bell:
Note: Math.random() does not provide cryptographically secure random numbers. Do not use them for anything related to security. Use the Web Crypto API instead, and more precisely the window.crypto.getRandomValues() method.
But don’t be mad at JavaScript. This method is implemented in the browser and varies depending on the engine. Chrome uses the V8 engine, which is open-source. Its pseudo random number generator is based on an algorithm called xorshift128+
static inline void XorShift128(uint64_t* state0, uint64_t* state1) {
uint64_t s1 = *state0;
uint64_t s0 = *state1;
*state0 = s0;
s1 ^= s1 << 23;
s1 ^= s1 >> 17;
s1 ^= s0;
s1 ^= s0 >> 26;
*state1 = s1;
}
Its name describes it pretty well: it consists of a couple of bitwise XORs and shifts applied to a 128-bit internal state.
Then the 64-bit int is converted to a double. To understand the process, let’s look at the structure of a double. Doubles consist of 64 bits: 1 bit sign, 11 bit exponent, 52 bit mantissa.

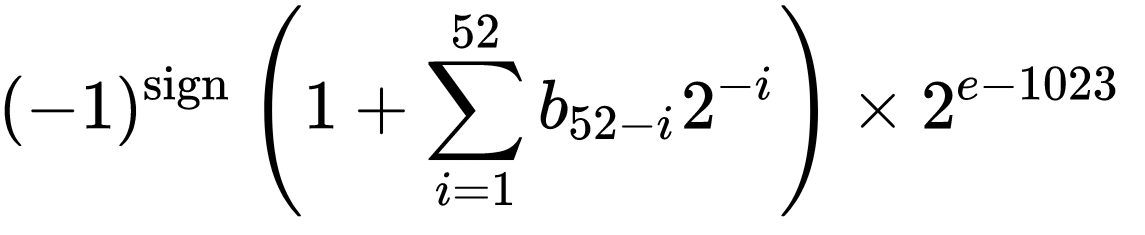
The end result is a double in the [0, 1) range. It is derived by manipulating the state0 value which is right shifted by 12 bits and ORed with 0x3FF0000000000000 setting the exponent to 01111111111 in binary, which is 1023. This produces a value between 1 and 2. Finally, 1 is subtracted to obtain a value in the range [0, 1).
static inline double ToDouble(uint64_t state0) {
static const uint64_t kExponentBits = uint64_t{0x3FF0000000000000};
uint64_t random = (state0 >> 12) | kExponentBits;
return bit_cast<double>(random) - 1;
}
In order to predict the next value, all we need is the 128 bit seed stored in state0 and state1. Our goal is to restore the seed from a list of consecutive outputs of the random number generator and predict the next value.
This problem can be tackled using Python and the Z3 library. Z3 is an SMT solver (Satisfiability Modulo Theories) capable of determining whether a set of mathematical expressions is satisfiable and determine a suitable set of inputs. This approach was already used in 2016 for cracking Math.random(), but a few things have changed since then. Firstly, the way of converting 64-bit ints into double was changed and described above. Secondly, instead of running the xorshift algorithm on every call, the new implementation uses a cache of 64 values. Calling Math.random() pops a value from this cache. When the cache becomes empty, it is refilled again with 64 values generated by xorshift. This means that the list of outputs should be reversed. Moreover, if the cache was refilled in the process of generating values, the list should be split into sublists corresponding to different caches and reversed. I will not implement this procedure to keep things simple.
Z3 works with symbolic values. The symbolic implementation of xorshift128+ is very similar to the C++ code above. Note that in Z3LShR is logical right shift and >> performs an arithmetic shift.
solver = z3.Solver()
state0, state1 = z3.BitVecs("state0 state1", 64)
def xs128p(state0, state1):
s1 = state0
s0 = state1
s1 ^= s1 << 23
s1 ^= z3.LShR(s1, 17)
s1 ^= s0
s1 ^= z3.LShR(s0, 26)
return s0, s1
Functions that are also needed are the Python versions of ToDouble and a function which does the opposite and converts doubles into 64-bit ints
def to_double(state0):
bits = (state0 >> 12) | 0x3FF0000000000000
return struct.unpack('d', struct.pack('<Q', bits))[0] - 1
def from_double(val):
return struct.unpack('<Q', struct.pack('d', val + 1))[0] & 0x3FFFFFFFFFFFFFFF
In the loop over each known output point, first the symbolic xorshift is executed. Then state0 is right shifted by 12 bits like in the ToDouble function, which produces the symbolic mantissa
points = points[::-1]
for point in points:
state0, state1 = xs128p(state0, state1)
calc = z3.LShR(state0, 12)
Our next goal is to set conditions on the generated mantissa calc. I am not aware of a straight-forward way of using floor rounding in this case, so the conditions are set for calc to be between a lower and upper value which are derived from point. The point value was generated by executing Math.floor(x * (max - min + 1)) + min, which allows us to determine the lower and upper bounds
def normalize(val):
return (val - min) / (max - min + 1)
lower = normalize(point)
upper = normalize(point + 1)
Then these values are converted into 64 bit ints using from_double
lower = from_double(normalize(point))
upper = from_double(normalize(point + 1))
The part that interests us is the mantissa, that is the last 52 bits. They are extracted by ANDing with 0x000FFFFFFFFFFFFF, which is 2^52 - 1
lower = lower & 0x000FFFFFFFFFFFFF
upper = upper & 0x000FFFFFFFFFFFFF
Finally, the condition is formulated and added to the solver
solver.add(z3.And(lower <= calc, calc <= upper))
Did you notice an edge case? With numbers close to the upper limit, calling from_double(normalize(point + 1)) may produce a number with an exponent of 1024 (not 1023) which will lead to a very different and invalid mantissa corresponding to a number greater or equal to 1 while Math.random() lies in [0, 1). This case should be checked. The exponent is extracted by right-shifting 52 bits to get rid of the mantissa, and the last 11 bits are selected by ANDing with 0x7FF (2^11 - 1)
upper_exp = (upper >> 52) & 0x7FF
The modified condition looks like this
z3.And(lower <= calc, z3.Or(calc <= upper, upper_exp == 1024))
The final loop that we get
for point in points:
state0, state1 = xs128p(state0, state1)
calc = z3.LShR(state0, 12)
lower = from_double(normalize(point))
upper = from_double(normalize(point + 1))
upper_exp = (upper >> 52) & 0x7FF
lower = lower & MANTISSA_MASK
upper = upper & MANTISSA_MASK
solver.add(z3.And(lower <= calc, z3.Or(calc <= upper, upper_exp == 1024)))
Now we should check for a valid solution. If it is found, the seed is extracted and the next random number can be predicted
if solver.check() == z3.sat:
model = solver.model()
state = {}
for d in model.decls():
state[d.name()] = model[d]
state0 = state["state0"].as_long()
state1 = state["state1"].as_long()
next = math.floor(to_double(state0) * (max - min + 1 )) + min
print(next)
Finally, we can predict the unpredictable. I have set the limits to min = 1 and max = 100000. The bigger the range, the fewer values are required to restore the seed because more information is preserved (a hefty chunk of bits is lost after math.floor). It required 10 generated values to work out the correct seed and predict the next value. It works!
As a web developer interested in cryptocurrency, I have heard about Math.random() being unsafe, and today I finally saw and tested a specific example proving this fact. Conclusion: please be aware that the Google random number generator is an unreliable source of entropy, especially for people familiar with bitwise operations.
Code: https://github.com/IvanLudvig/google-rng-hack
Sources:
https://blog.securityevaluators.com/hacking-the-javascript-lottery-80cc437e3b7f
https://github.com/d0nutptr/v8_rand_buster/